Topological insulators are a unique class of electronic materials that exhibit protected edge states that are insulating in the bulk, and immune to back-scattering and defects. Discrete models, such as mass-spring systems, provide a means to translate these properties, based on the quantum hall spin effect, to the mechanical domain. We are developing methods to engineer mechanical metamaterials that support topologically-protected and defect-immune edge states (vibrational modes), directly from the mass-spring model of a topological insulator. These metamaterials have potential applications as programmable waveguides, damage-tolerant materials, and elastic or heat lenses.
Current Work
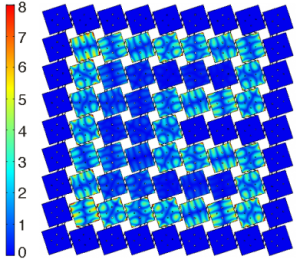
Mass-spring models provide a straightforward way to describe complex dynamic behavior of mechanical systems, such as the backscattering-free wave propagation in topologically insulating metamaterials. Such discrete models provide a means to translate these properties, based on the quantum hall spin effect, to the mechanical domain. However, there is currently no method to implement the behavior of a mass-spring model directly into a metamaterial, due to the immense design space of metamaterials and the complex interactions between vibrational modes of the unit cells. Here we address this problem by introducing “perturbative metamaterials”, i.e., metamaterials with weakly interacting unit cells. The weak interaction enables us to systematically convert mass-spring models to metamaterials, since it allows us to map geometric components of the metamaterial to masses and springs in the discrete model and quickly search the design space. Using this method, we design topologically insulating elastic metamaterials in 2D, by coupling structural modes of plates through soft beams. While we use this method to translate discrete models to elastic metamaterials with weak interactions, it can in principle be applied to other domains, e.g., acoustic, thermal, and photonic.
Journal Publications:
K.H. Matlack, M. Serra-Garcia, A. Palermo, S. D. Huber, C. Daraio. “Designing perturbative metamaterials from discrete models,” accepted by Nature Materials.
Conference Presentations:
K.H. Matlack, M. Serra-Garcia, A. Palermo, S. Huber, C. Daraio, “A metamaterial design method applied to topologically-protected mechanical metamaterials,” 174th Meeting of the Acoustical Society of America, Dec 4-8, 2017, New Orleans, LA (invited talk).
K.H. Matlack, M. Serra-Garcia, A. Palermo, S. Huber, C. Daraio, “A design method for topologically insulating metamaterials,” APS March Meeting, March 13-17, 2017, New Orleans, LA.
K.H. Matlack, M. Serra-Garcia, A. Palermo, S. Huber, C. Daraio, “Designing Topologically Insulating Metamaterials from Discrete Models”, Topological Metamaterials and Beyond, Aspen Center for Physics, Aspen, CO, January 2-8, 2017 (invited lecture).
