Phononic materials are engineered media that can manipulate waves propagating through them due to their synthetic and periodic architecture. However, phononic materials are mostly studied by assuming linear elasticity laws, which apply to small-amplitude waves only. Real-world materials experience high-amplitude excitations and can even exhibit enriched dynamic responses due to nonlinearity. How such high-amplitude mechanical waves interact with phononic media is at large under investigation and the primary focus of this project. In this work, we are developing a fundamental understanding of how waves evolve through nonlinear phononic materials, specifically through periodic local microstructures, e.g. rough contacts, inspired from geomaterials. The nonlinearity in our materials stems from the nonlinear mechanical deformation of the rough surfaces. We analyzed these materials through two approaches: 1) analytically by developing an equivalent discrete periodic model [Grinberg and Matlack, Wave Motion, 2020] and 2) numerically by considering a continuum with discrete contacts [Patil and Matlack, Wave Motion, 2021, Patil et al., Extreme Mechanics Letters, 2022, Patil and Matlack, Physical Review E, 2022, and Patil et al., Journal of Applied Mechanics, 2023]. Moreover, we considered the nonlinearity of rough contacts in both weakly and strongly nonlinear regimes, including friction, and studied its effect on wave propagation in continuum phononic material.
Discrete spring-mass model
We employed an equivalent discrete spring-mass model to understand the fundamental wave propagation characteristics of our nonlinear phononic material. Wave propagation was studied using a perturbation approach to obtain approximate analytical solutions and verified through full-scale numerical simulations. Our study focused on primary and secondary transmission characteristics, and showed that secondary transmission depends on the band structure of the underlying media, and also on system parameters such as the number of contacts, excitation amplitude, unit cell constant, and external precompression [Grinberg and Matlack, Wave motion, 2020].
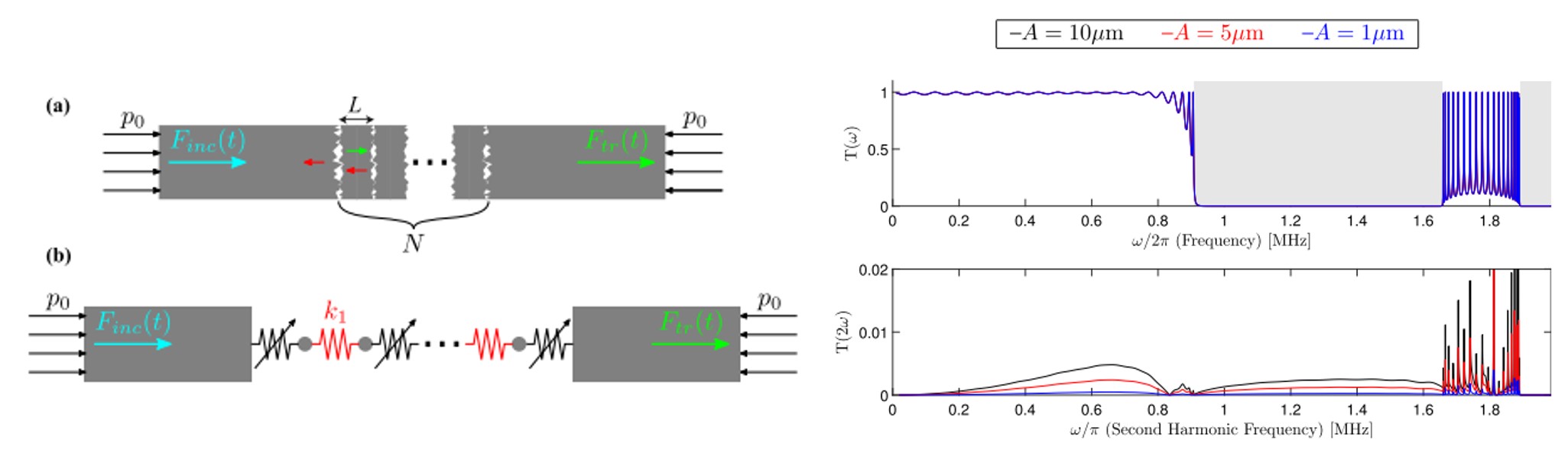
Continuum model with discrete nonlinearity
To understand the role of elastic deformation between nonlinear contacts, we simulated nonlinear wave propagation within a finite element framework. Our model revealed that the wave self-interaction with weakly nonlinear contacts generates zero- and second-harmonic frequencies, and also causes self-demodulation effects that generate very low frequencies. An interesting finding of the work was that the amplitude of these nonlinearly generated frequencies depends upon the local coupling of discrete contacts with the surrounding continuum and also on the contact distribution in the continuum [Patil and Matlack, Wave motion, 2021].
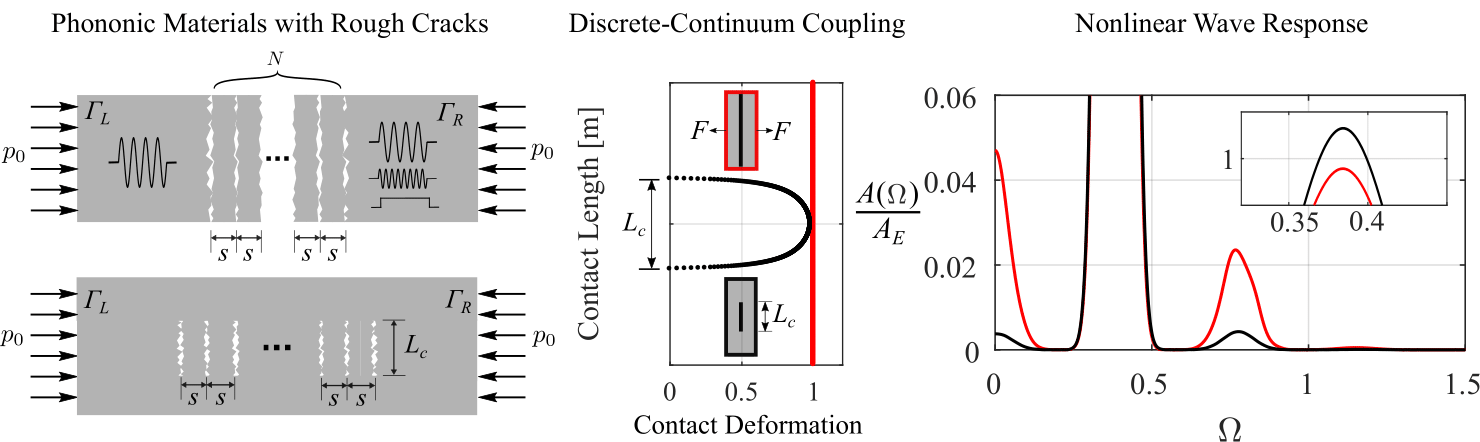
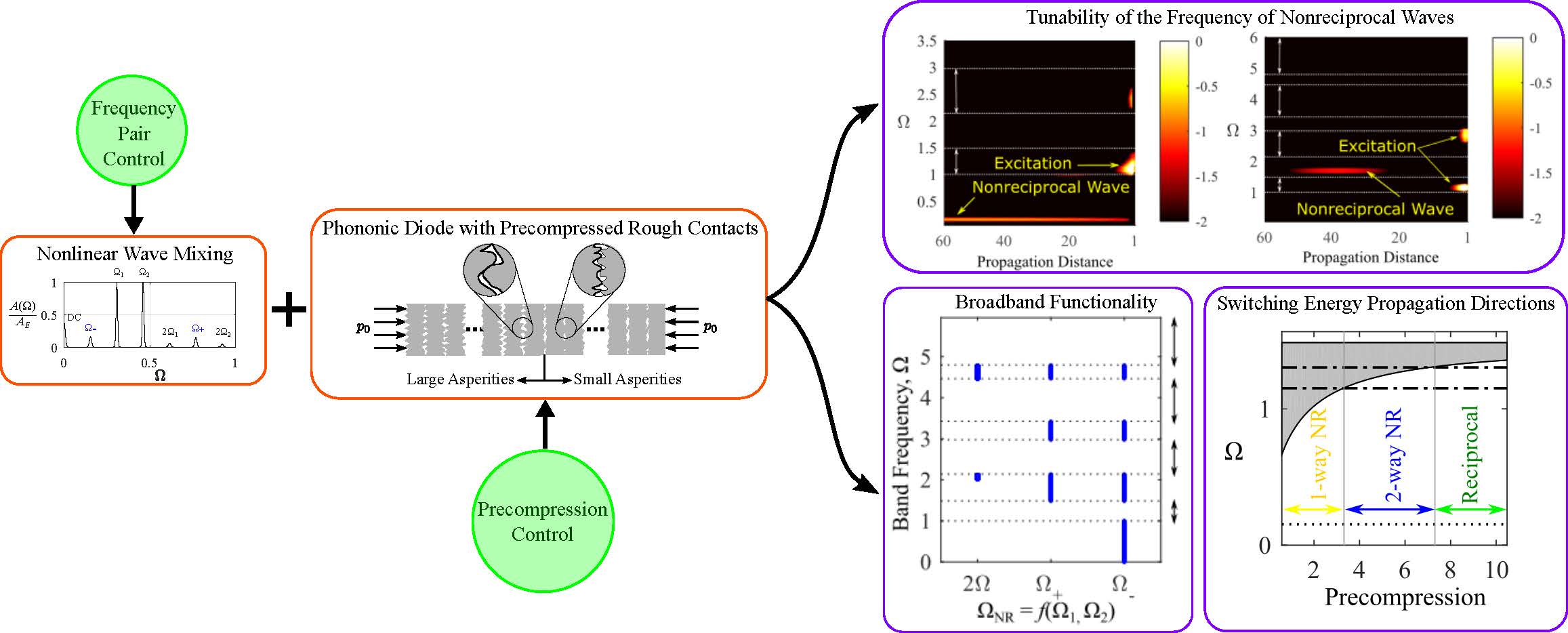
Using these weakly nonlinear features, we showed how wave mixing and nonlinear phononic materials can be combined together to design a phononic diode that can enable nonreciprocity over a broad frequency range [Patil et al., Ext. Mech. Lett., (2022)]. This diode also allows control over the frequency, mode, and direction of energy propagation of the nonreciprocal waves.
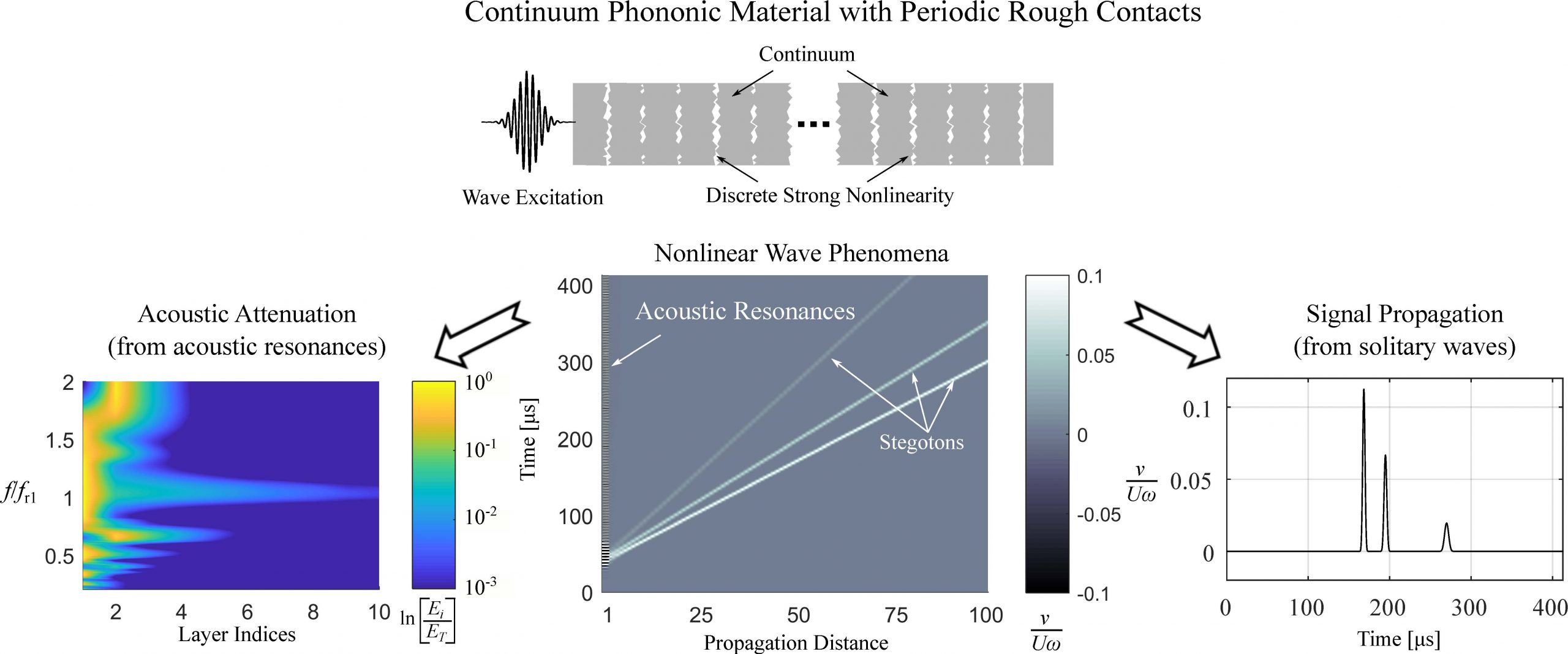
Further, our studies reveal that wave interaction with strongly nonlinear rough contacts enables rare phenomena of acoustic resonances and propagation of compact waves (named Stegotons). Resonances absorb the input energy providing design principles for protective equipment and shields, while compact waves carry energy long distances useful for designing mechanical sensors. Our study shows that materials designed by embedding discrete nonlinearity in a continuum are a promising route to enable multi-functionalities of energy absorption and acoustic signal propagation [Patil and Matlack, Physical Review E, 2022].
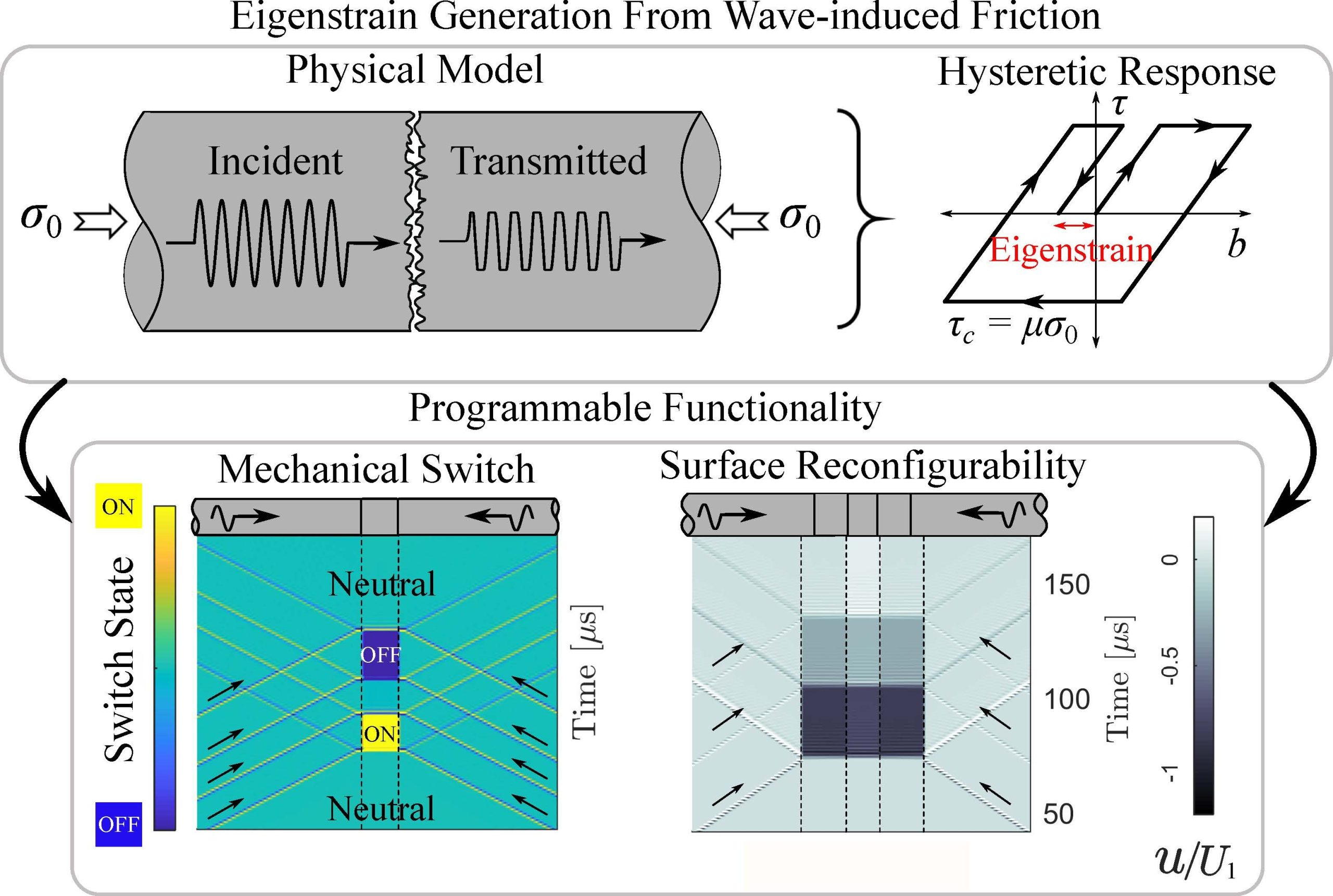
Additionally, we studied the role of frictional instability of rough contacts on wave manipulation. We revealed the emergence of eigenstrains, which are residual static deformations from the hysteretic contact response, under shear waves. By analyzing how these eigenstrains are generated in systems with periodic contacts, we demonstrated wave-governed programmable mechanical responses such as mechanical switches, precision actuation, and surface reconfigurability. These studies pave the way for the designing of smart materials and acoustic devices with advanced functionality.
This work was partially supported by the Army Research Office under Grant Number W911NF-20-1-0250
Journal Papers
- G. U. Patil, A. Fantetti, K. H. Matlack, Shear wave-induced friction at periodic interfaces for programmable mechanical responses. Journal of Applied Mechanics, 90(9), 091002 (2023). https://doi.org/10.1115/1.4062494
- G. U. Patil, Songyuan Cui, K. H. Matlack, Leveraging nonlinear wave mixing in rough contacts-based phononic diodes for tunable nonreciprocal waves. Extreme Mechanics Letters, 55, 101821 (2022). https://doi.org/10.1016/j.eml.2022.101821
- G. U. Patil, K. H. Matlack, Strongly nonlinear wave dynamics of continuum phononic materials with periodic rough contacts. Physical Review E, 105, 024201 (2022). https://doi.org/10.1103/PhysRevE.105.024201
- G. U. Patil, K. H. Matlack, Review of exploiting nonlinearity in phononic materials to enable nonlinear wave responses. Acta Mechanica, 233(1), 1-46 (2022). https://doi.org/10.1007/s00707-021-03089-z
- G. U. Patil, K. H. Matlack, Wave self-interactions in continuum phononic materials with periodic contact nonlinearity. Wave Motion, vol. 105, 102763 (2021). https://doi.org/10.1016/j.wavemoti.2021.102763
- I. Grinberg, K.H. Matlack, Nonlinear elastic wave propagation in phononic material with periodic solid-solid contact interface. Wave Motion, 93, 102466 (2020). https://doi.org/10.1016/j.wavemoti.2019.102466
Conference Proceedings
- G. U. Patil, K. H. Matlack, Nonlinear wave disintegration in phononic material with weakly compressed rough contacts, 10th European Nonlinear Oscillations Conference (2022). https://enoc2020.sciencesconf.org/382267/document
Conference Presentations
- G. U. Patil, K. H. Matlack*, Nonlinear wave propagation through phononic materials with rough contact interfaces, Phononics 2023: 6th International Conference on Phononic Crystals/Metamaterials/Metasurfaces, Phonon Transport, and Topological Phononics, Manchester, UK, Jun 2023 (Invited Talk)
- G. U. Patil*, A. Fantetti, K. H. Matlack, Frictional instability: a nonlinear mechanism to control shear wave responses in rough contact-based metamaterials, 183rd Meeting of the Acoustical Society of America, Nashville, TN, December 2022. https://doi.org/10.1121/10.0015463
- G. U. Patil*, K. H. Matlack, Nonlinear Wave Disintegration in Phononic Material with Weakly Compressed Rough Contacts, 10th European Nonlinear Dynamics Conference, Lyon, France, (July 2022). [Link]
- K. H. Matlack*, G. U. Patil, Nonlinear wave propagation from periodic arrangements of rough contact interfaces. 19th U.S. National Congress on Theoretical and Applied Mechanics, Austin, Texas, June 2022 (Invited Talk)
- G. U. Patil*, K.H. Matlack, Experimental study of nonlinear waves in phononic materials with rough contacts. 182nd ASA Meeting, Denver, Colorado, May 2022 https://doi.org/10.1121/10.0010593
- G. U. Patil*, K.H. Matlack, Emergence of stegotons in phononic materials with strongly nonlinear rough contacts. 181st ASA Meeting, Seattle, Washington, 30th November 2021 https://doi.org/10.1121/10.0007934.
- G. U. Patil*, K.H. Matlack, Tunable bandgaps and second harmonic generation of a one-dimensional nonlinear phononic material with periodic rough interfaces. The Virtual Meeting 2020 of the Society of Engineering Sciences (2020)
